- Beiträge
- 2.517
habe mich doch geirrt, im Skribt bei Punkt "3. Berechnung der Aufstandsflächen-Grenzkurve" wird der Thorus einbezogen.oder wo wird das genau einbezogen das er rund ist ?
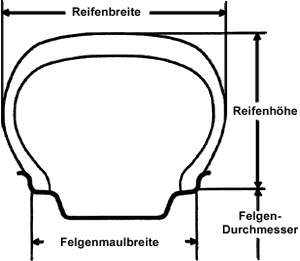
Man könnte statt dessen auch einen Michelin-Fahrrad-Radial-Reifen (= Rechteckiger Reifenquerschnitt) einberechnen. Da aber in den Eingangs-Voraussetzungen keine Walkung des Reifens angenommen wird, wird wohl kein großer Unterschied beim Endergebnis im Vergleich zum Thorus dabei herauskommen.
Gruß Leonardi