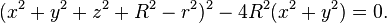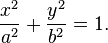- Beiträge
- 2.517
Das <Klick> brachte mir auf die Idee, das man die Ellipse = Reifenaufstandsfläche in Abhängigkeit von Reifenradius, Reifenbreite, Reifenluftdruck und Auflast rein theoretisch genau berechnen kann.
Der inneren Kräfte des Reifenmantels (das Bestreben die alte Form einzunehmen) haben bei unseren Reifenluftdrücken zB. 4 bar (= 4 kp/cm^2) eigentlich keinen Einfluss auf die Form und Größe der Reifenaufstandsfläche. Jedenfalls bei profilarmen Fahrradreifen. Ich lass das mal einfach so hingestellt.
Einfach mal mit dem Finger mit 4 kp/cm^2 auf einen aufgepumpten Reifen drücken und danach mit der gleichen Kraft auf einen Mantel ohne Luft drücken. Die inneren Kräfte des Reifenmantels sind viel geringer als die welche durch den Reifenluftdruck zustande kommen. Ich denke der Fehler ist gering, wenn man den Mantel als ganz dünn ohne innere Kräfte betrachtet, je höher der Reifenluftdruck desto geringer der Fehler.
Berechnung:
Die in obigen Link nur mit Phytagoras aufgestellte Gleichung für die Fläche des Reifenlatsches lautet
A_Latsch=pi/4*l*b = f (Radius Reifen R / Reifenbreite Radius r / Einsinktiefe s)
Der Reifen dellt sich je nach größe von F_Auflast bis auf die Fläche A_Latsch ein. Das ganze hängt vom Reifenluftdruck p ab. Es gilt p=F/A bzw. F_Auflast/p = A_Latsch = f(R/r/s) nochmal:
F_Auflast / p = A_Latsch = f(R/r/s) wobei alle Werte gegeben sind, nur s die Einsinktiefe wird gesucht.
Stellt man die Gleichung nach s um, so gibt sich unter der Vereinfachung s^2 << 2*R*s
(etwa das Verhältnis 1:1000, macht also als Fehler nur 1/1000 aus) eine kubische Gleichung. Wenn man nicht Vereinfacht gibt es eine quartische Gleichung. Die ist auch lösbar, hatte ich aber keine Lust dazu.
Jedenfalls hat man als Lösung die Einsinktiefe aus welcher man wieder die Ellipsen Halbachsen l und b rückrechnet.
Sieht dann so aus, in den gelben Feldern müssen die Werte eingegeben werden (Sehe gerade ETRTO muss es heißen, ein T vergessen):
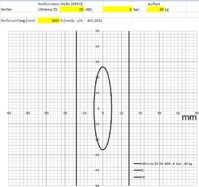
Jetzt werden manche fragen, was dies denn bringt. Nun zum Beispiel kann man davon ausgehen, das auf ganz glatter Straße eine gleiche Reifenaufstandsfläche den gleichen Rollwiderstand entspricht, wo keine Steinchen oder Löcher zusätzliche Verforumgsverluste bringen.
Die Reifenaustandsfläche von 4 bar und 40 kg Auflast lässt sich zB. auch bei einer höheren Auflast (muss mal Schieberegler ranmachen) durch einen höheren Reifenluftdruck erzeugen. Wenn also jemand wissen möchte wieviel er zupumpen muss um bei der Ferienfahrt genau so leicht zu rollen.
Man kann auch durch Erhöhung des eingegebenen Reifenluftdrucks beobachten, das die Reifenaufstandsfläche am Ende immer unwesentlicher kleiner wird. A_Aufstandsfläche wird auch in Excel ausgegeben.
***
An Reifenlatsch Berechnungen finde ich sonst nur das: http://www.faltradforum.de/viewtopic.php?p=22667#p22667 Da wurde ein realer Abdruck mit roter Stempelfarbe auf einem Papierblatt erzeugt, die Halbachsen der Ellipse l und b gemessen. Der Vergleich mit der theoretischen Berechnung ergab ausgezeichnete Übereinstimmung (auch deshalb schrieb ich das die inneren Kräfte des Reifens vernachlässigbar sind) - sehe aber auf die schnelle nicht wie das theoretisch berechnet wurde.
Bei mir könnte auch ein Flüchtigkeitsfehler im anliegenden Excel.zip sein, keine Zeit für Prüfung gehabt. Muss auch mal mehrere Reifen bzw. Variablen gleichzeitig darstellbar machen, später mal.
Gruß Leonardi
Der inneren Kräfte des Reifenmantels (das Bestreben die alte Form einzunehmen) haben bei unseren Reifenluftdrücken zB. 4 bar (= 4 kp/cm^2) eigentlich keinen Einfluss auf die Form und Größe der Reifenaufstandsfläche. Jedenfalls bei profilarmen Fahrradreifen. Ich lass das mal einfach so hingestellt.
Einfach mal mit dem Finger mit 4 kp/cm^2 auf einen aufgepumpten Reifen drücken und danach mit der gleichen Kraft auf einen Mantel ohne Luft drücken. Die inneren Kräfte des Reifenmantels sind viel geringer als die welche durch den Reifenluftdruck zustande kommen. Ich denke der Fehler ist gering, wenn man den Mantel als ganz dünn ohne innere Kräfte betrachtet, je höher der Reifenluftdruck desto geringer der Fehler.
Berechnung:
Die in obigen Link nur mit Phytagoras aufgestellte Gleichung für die Fläche des Reifenlatsches lautet
A_Latsch=pi/4*l*b = f (Radius Reifen R / Reifenbreite Radius r / Einsinktiefe s)
Der Reifen dellt sich je nach größe von F_Auflast bis auf die Fläche A_Latsch ein. Das ganze hängt vom Reifenluftdruck p ab. Es gilt p=F/A bzw. F_Auflast/p = A_Latsch = f(R/r/s) nochmal:
F_Auflast / p = A_Latsch = f(R/r/s) wobei alle Werte gegeben sind, nur s die Einsinktiefe wird gesucht.
Stellt man die Gleichung nach s um, so gibt sich unter der Vereinfachung s^2 << 2*R*s
(etwa das Verhältnis 1:1000, macht also als Fehler nur 1/1000 aus) eine kubische Gleichung. Wenn man nicht Vereinfacht gibt es eine quartische Gleichung. Die ist auch lösbar, hatte ich aber keine Lust dazu.
Jedenfalls hat man als Lösung die Einsinktiefe aus welcher man wieder die Ellipsen Halbachsen l und b rückrechnet.
Sieht dann so aus, in den gelben Feldern müssen die Werte eingegeben werden (Sehe gerade ETRTO muss es heißen, ein T vergessen):

Jetzt werden manche fragen, was dies denn bringt. Nun zum Beispiel kann man davon ausgehen, das auf ganz glatter Straße eine gleiche Reifenaufstandsfläche den gleichen Rollwiderstand entspricht, wo keine Steinchen oder Löcher zusätzliche Verforumgsverluste bringen.
Die Reifenaustandsfläche von 4 bar und 40 kg Auflast lässt sich zB. auch bei einer höheren Auflast (muss mal Schieberegler ranmachen) durch einen höheren Reifenluftdruck erzeugen. Wenn also jemand wissen möchte wieviel er zupumpen muss um bei der Ferienfahrt genau so leicht zu rollen.
Man kann auch durch Erhöhung des eingegebenen Reifenluftdrucks beobachten, das die Reifenaufstandsfläche am Ende immer unwesentlicher kleiner wird. A_Aufstandsfläche wird auch in Excel ausgegeben.
***
An Reifenlatsch Berechnungen finde ich sonst nur das: http://www.faltradforum.de/viewtopic.php?p=22667#p22667 Da wurde ein realer Abdruck mit roter Stempelfarbe auf einem Papierblatt erzeugt, die Halbachsen der Ellipse l und b gemessen. Der Vergleich mit der theoretischen Berechnung ergab ausgezeichnete Übereinstimmung (auch deshalb schrieb ich das die inneren Kräfte des Reifens vernachlässigbar sind) - sehe aber auf die schnelle nicht wie das theoretisch berechnet wurde.
Bei mir könnte auch ein Flüchtigkeitsfehler im anliegenden Excel.zip sein, keine Zeit für Prüfung gehabt. Muss auch mal mehrere Reifen bzw. Variablen gleichzeitig darstellbar machen, später mal.
Gruß Leonardi
Anhänge
Zuletzt bearbeitet: