- Beiträge
- 3.485
Hallo zusammen!
Mich ärgert schon seit langem, dass es in Diskussionen immer wieder nur um die Watt geht, um eine bestimmte Geschwindigkeit zu halten – das ist erstens irreführend, weil die Leistung sehr stark von vielen Umgebungsbedingungen abhängt, und zweitens realitätsfern, weil eine konstante hohe Geschwindigkeit im Alltag und Rennen kaum vorkommt.
Darum habe ich mein Powermeter-Diagramm umgebaut, so dass man die Strecke und Umgebungsbedingungen frei einstellen kann; das Ergebnis ist der:
(Der Name ist etwas irreführend; man kann damit beliebige Fahrräder simulieren und auch andere Fahrzeuge, solange man weiß, was man tut. Aber bei Velomobilen sind besonders die aerodynamischen Parameter recht konstant, statt z.B. von der Figur und Kleidung des Fahrers abzuhängen, daher ist das besonders gut geeignet.)
Es handelt sich um ein Diagramm, bei dem die Fahrwiderstände mit den gleichen Formeln wie beim Kreuzotter-Rechner berechnet werden (die entsprechende Diskussion ist hier). Lediglich bei den Antriebsverlusten verwende ich eine andere Konvention; während diese bei Kreuzotter auf die benötigte Leistung draufgeschlagen werden, ziehe ich sie von der Tretleistung ab, d.h. 8% Antriebsverluste bedeuten, dass 92% der Tretleistung nutzbar sind.
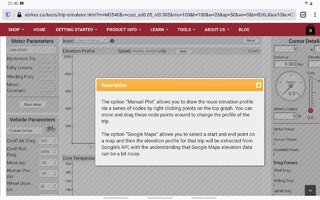
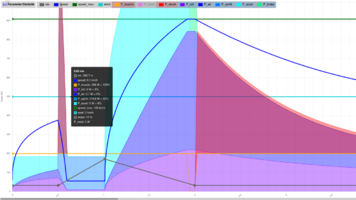
Hier eine kurze Beschreibung. Erstens das Bild nach dem Start:
Aufbau des Diagramms:
Interpretation Teil 1:
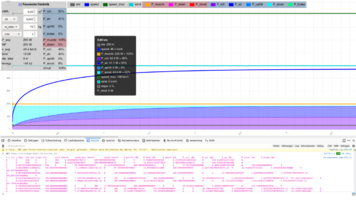
Was vielleicht auch noch ganz interessant ist: Wenn der Parameter csv auf 1 gesetzt ist, wird in die Browser-Konsole eine Tabelle mit allen Datenwerten geschrieben. Die kann man dann z.B. in die Tabellenkalkulation laden und weiterverarbeiten (hier Beispiel Firefox):
Und wozu das Ganze? Man kann mit verschiedenen Szenarien herumspielen:
Der versionierte Quellcode findet sich übrigens hier im Git.
Mich ärgert schon seit langem, dass es in Diskussionen immer wieder nur um die Watt geht, um eine bestimmte Geschwindigkeit zu halten – das ist erstens irreführend, weil die Leistung sehr stark von vielen Umgebungsbedingungen abhängt, und zweitens realitätsfern, weil eine konstante hohe Geschwindigkeit im Alltag und Rennen kaum vorkommt.
Darum habe ich mein Powermeter-Diagramm umgebaut, so dass man die Strecke und Umgebungsbedingungen frei einstellen kann; das Ergebnis ist der:
(Der Name ist etwas irreführend; man kann damit beliebige Fahrräder simulieren und auch andere Fahrzeuge, solange man weiß, was man tut. Aber bei Velomobilen sind besonders die aerodynamischen Parameter recht konstant, statt z.B. von der Figur und Kleidung des Fahrers abzuhängen, daher ist das besonders gut geeignet.)
Es handelt sich um ein Diagramm, bei dem die Fahrwiderstände mit den gleichen Formeln wie beim Kreuzotter-Rechner berechnet werden (die entsprechende Diskussion ist hier). Lediglich bei den Antriebsverlusten verwende ich eine andere Konvention; während diese bei Kreuzotter auf die benötigte Leistung draufgeschlagen werden, ziehe ich sie von der Tretleistung ab, d.h. 8% Antriebsverluste bedeuten, dass 92% der Tretleistung nutzbar sind.
Hier eine kurze Beschreibung. Erstens das Bild nach dem Start:

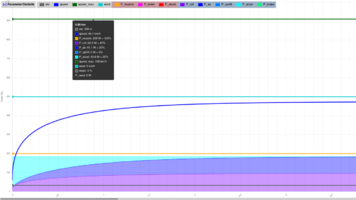
Aufbau des Diagramms:
- Nach rechts wird die Entfernung angezeigt (in km).
- Nach oben die zugehörigen Eigenschaften; beschriftet ist hier nur die Leistung. Die Höhe und die Geschwindigkeit verwenden andere Skalen, d.h. hier darf man sich nicht an den Gitterlinien der Leistung orientieren.
- Die vier waagerechten Linien sind die Eingabedaten; von unten nach oben:
- grau: Höhe (bezogen auf die Basishöhe)
- gelb: Tretleistung
- türkis: Windgeschwindigkeit
- dunkelgrün: Maximalgeschwindigkeit
- Daraus berechnet wird die Geschwindigkeit; das ist die blaue Kurve.
- => In der Voreinstellung hat man also einen 75 kg schweren Fahrer mit 30 kg Velomobil, der auf vollkommen ebener Strecke bei Windstille konstant 200 W tritt.
- Die farbigen Flächen unten zeigen die daraus berechneten Leistungswerte. Die Farben sind oben in der Legende sichtbar.
- Dabei sind die rötlich hinterlegten Kurven die Eingangsleistung, die blau hinterlegten Kurven die Ausgangsleistung.
- => Es gibt also zwei Sätze von gestapelten Leistungskurven, die gleich hoch sind.
- Bei Klick auf die Legende kann man einzelne Kurven aus- bzw. einblenden.
- An der Position des Mauszeigers werden alle Daten an diesem Punkt angezeigt. (Wird ein Wert nicht angezeigt, dann ist er 0.)
- Zu fast allen Elementen gibt es Tooltips mit einer kurzen Erklärung.
- Der Fahrer tritt mit der durch die gelbe Linie angegebenen Leistung.
- Die violette Fläche ist der Rollwiderstand, die bläuliche Fläche darüber der Luftwiderstand. Beide steigen mit der Geschwindigkeit an.
- Die verbleibende Fläche unter der gelben Linie steht für die Beschleunigung zur Verfügung. Das wird durch die helltürkise Fläche gezeigt.
- => Hier sieht man gut, warum die Beschleunigung auf hohe Geschwindigkeiten so lange dauert: es bleibt immer weniger Beschleunigungsleistung übrig, weil Roll- und Luftwiderstand mit steigender Geschwindigkeit einen immer größeren Anteil einnehmen.
- Die Flächen dieser drei Verlustleistungen reichen nicht ganz bis zur Tretleistung hinauf, sondern es bleibt eine Lücke. Das sind die Antriebsverluste; in der Voreinstellung 8%.
- Durch Klick auf eine der Eingabekurven wird ein Datenpunkt hinzugefügt.
- Diesen kann man mit der Maus beliebig verschieben.
- Durch Klick auf einen dieser Datenpunkte wird er wieder gelöscht.
- Mit den Pfeiltasten und Pos1/Ende kann man scrollen.
- Mit +/- kann man zoomen.

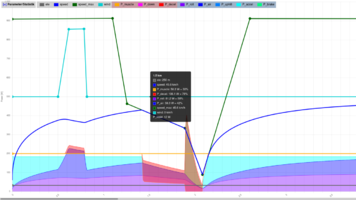
Interpretation Teil 1:
- Hier wird als erstes die türkise Kurve der Windgeschwindigkeit verändert.
- Diese ist normalerweise 0; wird die Kurve nach oben gezogen, bedeutet es Gegenwind; nach unten = Rückenwind.
- Hier herrscht zuerst Windstille, aber dann kommt für wenige 100 m ein starker Gegenwind auf.
- Man sieht unten, dass der Rollwiderstand gleich bleibt, aber der Luftwiderstand deutlich nach oben geht.
- Die Summe aus Roll- und Luftwiderstand übersteigen sogar die gelbe Kurve der Tretleistung.
- Die fehlende Leistung ist dann diese rote Fläche; das ist P_decel, d.h. die fehlende Leistung kommt aus der Bewegungsenergie, und entsprechend sinkt die Geschwindigkeit. (Die rote Fläche überragt das obere Ende der Luftwiderstandskurve; das sind wieder die Antriebsverluste.)
- Sobald der Wind weg ist, ist die Situation wie vorher, die Beschleunigung geht weiter, die Geschwindigkeit steigt wieder.
- Weiter rechts im Bild wird die dunkelgrüne Kurve der Maximalgeschwindigkeit verändert.
- Anfangs macht das nichts; aber wenn die grüne Kurve auf die blaue Geschwindigkeitskurve trifft, wird diese mit nach unten gezogen.
- Entsprechend reduzieren sich Roll- und Luftwiderstand.
- Da dann auch keine Beschleunigungsleistung anfällt, sondern umgekehrt Bewegungsenergie frei wird, sinkt der Leistungsbedarf.
- Entsprechend ist zwar die gelbe Soll-Kurve der Tretleistung weiterhin bei 200 W, aber wie man im Tooltip sehen kann, werden nur noch 50 W Tretleistung benötigt, die restliche Leistung stammt aus der Bewegungsenergie (106 W).
- Etwas weiter rechts geht die dunkelgrüne Tempolimit-Kurve noch einmal steiler nach unten.
- Entsprechend wird sehr viel Bewegungsenergie frei – die rote Fläche erzeugt einen großen Zacken nach oben.
- Da dieser Zacken die Summe aus Rollwiderstand, Luftwiderstand und Antriebsverlust jetzt deutlich übersteigt, gibt es einen großen Leistungsüberschuss, der nicht mehr alleine durch die Reduktion der Tretleistung auf 0 kompensiert werden kann.
- Wenn man die rote P_decel-Kurve ausblendet, sieht man, was das ist: dort befindet sich ein grüner Zacken – das ist die Bremsleistung. Hier muss also gebremst werden.
- Wenn danach die Maximalgeschwindigkeit wieder ansteigt, beschleunigt das Velomobil wieder wie am Anfang.

- Zwischen 0.5 und 2 km gibt es einen Berg, der mit 10% ansteigt und dann mit etwa 5% abfällt (graue Kurve).
- Am Fuß des Berges steigt der Leistungsbedarf sehr stark an (erster Zacken), weit über die verfügbare Tretleistung.
- Die entsprechende Leistung wird aus der Bewegungsenergie genommen; entsprechend bricht die Geschwindigkeit massiv ein, damit aber auch der Leistungsbedarf.
- Es geht im Schneckentempo bergauf; dort reichen die 200 W Tretleistung, die weitgehend für die Kletterarbeit (blaugraue Fläche) verwendet wird. Der Rollwiderstand ist nur noch klein, der Luftwiderstand fast 0.
- Bergab wird dann sehr viel Leistung frei (P_down, hier ausgeblendet); weil diese viel größer als Roll- und Luftwiderstand und Antriebsverlust ist, geht der Löwenanteil in die Beschleunigung (türkise Fläche). Entsprechend rasant steigt die Geschwindigkeit.
- Am Ende des Gefälles wird die Maximalgeschwindigkeit erreicht; hier bricht die Tretleistung wieder auf 0 ein und es muss gebremst werden (grüne Fläche oben, wo die Geschwindigkeitskurve abgeschnitten ist).
- In der Ebene reicht die Tretleistung bei weitem nicht, um die Fahrwiderstände zu kompensieren; entsprechend kommt der größte Teil der Leistung aus der Bewegungsenergie (rote Fläche oberhalb der Tretleistung), und die Geschwindigkeit fällt.
- D.h. es gibt immer zwei gestapelte Flächen, die überlappend dargestellt werden und gleich groß sind:
- Eingangsleistung: Tretleistung + Bergab-Leistung + Leistung aus der Geschwindigkeitsreduktion
- Ausgangsleistung: Rollwiderstand + Luftwiderstand + Antriebsverlust + Beschleunigung + Kletterarbeit + Bremsen
Was vielleicht auch noch ganz interessant ist: Wenn der Parameter csv auf 1 gesetzt ist, wird in die Browser-Konsole eine Tabelle mit allen Datenwerten geschrieben. Die kann man dann z.B. in die Tabellenkalkulation laden und weiterverarbeiten (hier Beispiel Firefox):

Und wozu das Ganze? Man kann mit verschiedenen Szenarien herumspielen:
- z.B. schauen, wie viel Zeitersparnis eine Optimierung an Roll- oder Luftwiderstand oder auch Gewicht bringt
- z.B. schauen, wie man sich seine Leistung einteilen muss, um bei gleicher Gesamtenergie möglichst schnell am Ziel zu sein ...
- ... und dabei die Normalized Power (NP) nicht zu sehr ansteigen lässt
- Die Berechnung scheint grundsätzlich recht sinnvolle Werte zu liefern.
- Aber wenn man in den Parametern irgendwelche unrealistischen Extremwerte einträgt, dann kann es schon sein, dass die Berechnung kapituliert.
- Die Bedienung mit der Maus ist manchmal hakelig. Mal sehen, ob ich das irgendwann verbessern kann.
- Die Farben sind nicht ganz optimal, manche sind zu ähnlich. Aber da es viele sind, gibt es da keine simple Lösung.
- Man kann noch nicht alle Werte dynamisch ändern, z.B. die Diagramm-Breite.
Der versionierte Quellcode findet sich übrigens hier im Git.